Everyone likes to save money–and when you’re running a huge business like Zalando, saving money by making your systems more efficient can mean saving millions of Euros. That’s why I’m excited to tell you that the Zalando Data Intelligence team recently found a way to save us piles of money. In this post, I’ll tell you how.
THE GOAL
Until recently, the only way that Zalando’s warehouse workers were able to determine the weights of our hundreds of thousands of items was by weighing each item manually. As you can imagine, this was a labor-intensive, time-consuming and expensive process.
It recently occurred to us that we could greatly simplify our operations by replacing our manual weight estimation process with highly refined data from another, automatic process. Here’s where those huge savings for Zalando appears: By accurately inferring the individual item weights from the parcel weights, we save A LOT of Euros–and a lot of our workers’ time.
THE FREE DATA
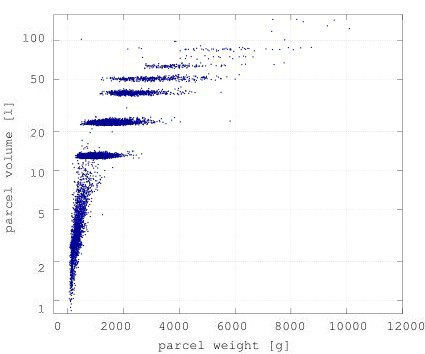
The key here is that we already have data for free on the volume and weight of every parcel that leaves the Zalando warehouse. After a parcel is packed but before it is given to our logistics partners (like DHL) for delivery to the customer, its volume and weight are automatically measured. We just need to somehow get the individual article weights from this data. The figure below shows the weights and volumes of some parcels that were measured:
Figure 1: Weights and volumes of parcels sent from the Zalando warehouse, as measured by the volume scanner. The parcels with a low weight and highly varied volume are envelopes, and the volume of the envelope varies with the volume of the contents.
THE NAIVE METHOD
#One of the most basic methods we could use to infer item weights from parcel weights works like this: Say we send out three parcels with the inferred weights [latex]p1[/latex],[latex]p2[/latex],[latex]p3[/latex], and three items with the inferred weights [latex]w1[/latex],[latex]w2[/latex], and [latex]w3[/latex]. Since the warehouse software tracks which items were in which parcels, we get the following linear equation:
- The outbound scale is prone to measurement errors
- We don’t always know the exact packaging type (the type of cardboard box) that the items were packed into
- We don’t always know how much packing material, vouchers, and other stuff is included in the individual parcels
- Because there are far more parcels than items, and a lot of little unknowns and measurement errors along the way, the matrix [latex]A[/latex] doesn’t have a true inverse
- There are some articles where we don’t have enough information to accuracy estimate an article’s weight. Therefore our goal is to calculate not just point estimates but also confidence intervals so that we know how sure we can be about our estimate of an article’s weight.
Because of Zalando’s massive size and speed of operations, we need a much cleaner, more accurate method. For this, our data intelligence team turned to Bayesian statistics. In our next tech blog article we’ll go into the mathematical details of the Baysian model we used. If you want to see a cool example of statistical modeling in action, the next article is perfect for you. But this is the fluffy non-technical article, so we’ll go straight to showing you how awesome our weight estimation method is.
Results
There are many different criteria for evaluating accuracy, so let’s look at how our weight estimator performed compared to various evaluation criteria.
Measured vs. Estimated
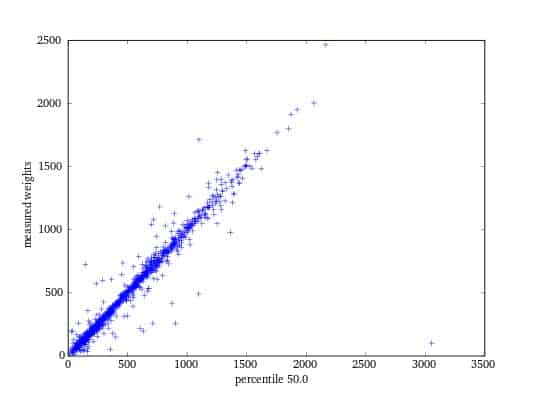
Many Zalando items have already been weighed manually, so a natural evaluation strategy would be to compare the measured weight of an article against its estimated weight:
Figure 2: Estimated article weights vs. the weight obtained by weighing actual article
Pretty good, but there are still some errors. The next few sections explore why we believe that many of these errors came about from manual measuring, not from our weight estimator.
Net Parcel Weights
Another way to gain a stronger understanding of how our estimator performs is to subtract the weight of each parcel from the estimated weights of the items inside that parcel. Then we can see how the differences cluster around the true packaging weights.
Figure 3 shows the results of our manual process, in which we subtracted the measured items’ weights. This revealed two important things:
- Many parcels have a negative weight once the item weights have been subtracted. Clearly this can not be the case–there must be an error in the system somewhere.
- The net weights vary widely, and don’t cluster nicely.
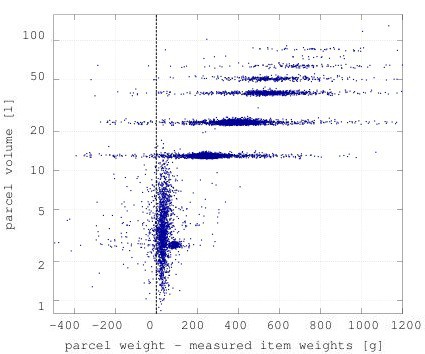
Figure 3: The volumes and weights of parcels after we subtracted the weight of the items in the parcel, where the item weights were obtained via a manual weighing process.
Instead of using the article weights obtained by the manual process, we used the article weights obtained by our weight estimator; this is illustrated by Figure 4. Almost all net parcel weights are greater than zero, and the parcels cluster into small balls.
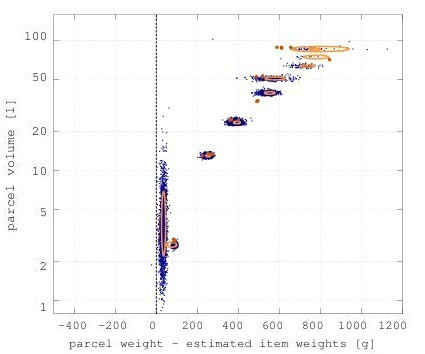 Figure 4: The volumes and weights of parcels after we subtracted the weight of the items in the parcel, where the item weights were obtained via our weight estimator. The orange lines represent where most of the mass of the clusters lie
Figure 4: The volumes and weights of parcels after we subtracted the weight of the items in the parcel, where the item weights were obtained via our weight estimator. The orange lines represent where most of the mass of the clusters lie
Confidence Intervals
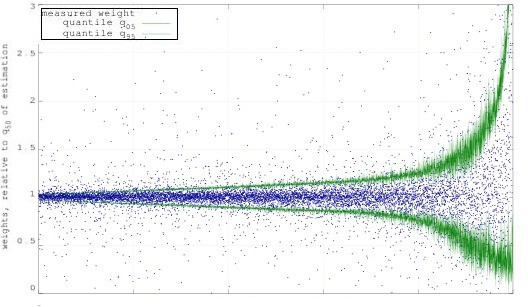
If you remember back, we didn’t just want to produce estimates of article weights, but also wanted to generate so-called confidence intervals. A confidence interval is when we can say that an article weighs between 150 and 170 grams with a 90% probability. Our automated weight estimator delivers results that nicely fit the data.
In Figure 5, each blue dot represents an estimated article weight. The position of particular dots on the y-axis is the relative error defined as
Figure 5: Plot showing different relative errors in weight estimations and the confidence in the weight estimations. We see that for the vast majority of cases, the estimation lies between the confidence intervals.
The Payoff
Deriving our new measuring model and verifying that it works took some effort! But it was all worth it, because now we have:
- Automatic weight estimations for each Zalando article, which saves workers time
- A reliable way to know the accuracy of our estimations
And most importantly: our warehouse workers can now focus on getting your fashion to you as quickly as possible. That’s isn’t just saving money–that’s priceless.
If you liked this post, be sure to read (and like) the next article with all the great mathematical details of our Bayesian model.
This post was written by Calvin Seward, Urs Bergmann and Roland Vollgraf from the data science team at Zalando, and originally appeared here. The Bayesian model was developed by Roland Vollgraf- Zalando’s Data Science Expert- with Urs as an important collaborator.
Featured image credit: tech.eu








The obvious question probably is: Does that really save the worker’s time or do you just not hire as many as before?
Second obvious question: What do you need the item weight for, if the outbound weight of parcels is already determined? I can picture some uses, like predicting how costly each item is to ship, on average. but that’s just speculation.