Many of today’s technologies are based on the principle of giving an output to an input. But did you know this principle is based on Finite-State Machines?
The allure of AI often enthralls our imagination, painting vivid pictures of intelligent machines capable of human-like cognition and decision-making. Yet, before delving into the complexities of advanced AI systems, we must pay homage to the ancestors of AI, and none is more significant than the Finite-State Machine. This elegantly simple mathematical construct serves as a cornerstone, influencing the very essence of AI technologies as we know them today.
At its core, the Finite-State Machine is a captivating model that thrives on the principles of discrete states and transitions. Its architecture comprises a finite set of states, an array of input symbols, an optional set of output symbols, and a collection of rules that govern the transitions between states, all orchestrated with a masterful simplicity that belies its power.

What is Finite-State Machine?
A Finite-State Machine (FSM) is a fundamental concept in the world of computer science and engineering. It serves as a mathematical model that allows us to represent and control systems with discrete states and transitions. This powerful abstraction is widely used in various fields, from hardware design and software development to robotics and artificial intelligence.
At its core, an FSM is composed of several key components that define its behavior and functionality. These components include:
States: The FSM operates within a finite set of states, each representing a specific condition or situation in the system being modeled. These states act as snapshots of the system’s state at different points in time, reflecting its internal configuration or behavior.
Input symbols: The FSM interacts with the external environment through a set of input symbols. These symbols can be any form of input data, such as characters, numbers, or even sensory data from sensors in a robotic system.
Output symbols: In some cases, an FSM may also have a set of output symbols associated with transitions between states. These output symbols represent the machine’s response to specific inputs and can be used to communicate information or trigger actions in the system.
How artificial intelligence went from fiction to science?
Transition rules: The heart of the FSM lies in the set of rules that dictate how it transitions from one state to another based on the input symbols it receives. These rules, often represented as a transition table or a state diagram, define the behavior and logic of the system being modeled.
The operation of an FSM can be visualized as a dynamic flow between states driven by the input symbols it processes. When the machine starts, it enters an initial state, which serves as the starting point for its computation. As it reads each input symbol, it applies the predefined rules to determine the next state. This process continues until the Finite-State Machine reaches a final state, signifying the completion of a specific task, or it halts due to an undefined transition.
Finite-State Machines have applications in various domains due to their simplicity, efficiency, and versatility. In hardware design, FSMs are used to control digital circuits, enabling devices like microcontrollers, processors, and memory units to perform specific tasks based on input signals. In software development, FSMs play a crucial role in tasks such as lexical analysis, parsing, and regular expression matching.

Who is the founder of Finite-State Machines?
The founder of the finite-state machine is Edward Forrest Moore. He was an American professor of mathematics and computer science, and he invented the Moore finite state machine in 1956. Moore’s work was based on the earlier work of Warren McCulloch and Walter Pitts, who had proposed a mathematical model of the human brain in 1943.
Moore’s finite state machine is a type of finite automaton that has a single output value for each state. This is in contrast to the Mealy finite state machine, which has a separate output value for each input-state pair. Moore’s finite state machines are simpler to implement than Mealy machines, and they are often used in digital circuits and software.
What are the different types of Finite-State Machines?
Finite-State Machines (FSMs) come in various types, each offering unique characteristics and functionalities that cater to specific applications. Understanding these different types is crucial for designing efficient and effective systems.
Deterministic Finite-State Machines (DFSM)
Deterministic Finite-State Machines are the most straightforward and common type of FSMs. In a DFSM, for every state and input symbol, there is precisely one defined transition to the next state. This deterministic behavior means that given a specific input symbol and the current state, the machine will always transition to the same next state. The transition is unambiguous, leading to a predictable outcome.
DFSMs are particularly useful in applications where the behavior needs to be well-defined and where certainty in the machine’s operation is essential. They excel in scenarios that require precise control and where there is no need for branching or multiple possible outcomes based on the same input symbol.
Non-deterministic Finite-State Machines (NFSM)
Non-deterministic Finite-State Machines, in contrast to DFSMs, allow multiple transitions from a state for a given input symbol. This non-determinism introduces branching and ambiguity in the machine’s behavior, as there can be different possible paths that the machine can follow based on the same input symbol and current state.
NFSMs are advantageous in situations where there are multiple valid choices or decisions that can be made based on the same input. They provide a more flexible and expressive representation, enabling the FSM to explore various possibilities simultaneously. This characteristic is especially useful in complex applications that involve decision-making, problem-solving, and search algorithms.

Mealy Machines and Moore Machines
Apart from the distinction between deterministic and non-deterministic FSMs, there are two additional categories based on how the output is determined during transitions:
- Mealy Machines
- Moore Machines
Mealy Machines
In Mealy Machines, the output is determined by both the current state and the input symbol during transitions. This means that the output is associated with the transitions between states rather than being linked solely to the current state. As a result, Mealy Machines tend to have more compact representations as they do not need to associate output with each state.
Mealy Machines are often employed in applications where the output is directly related to the input and the machine’s behavior requires responsiveness to changes in input symbols. They are well-suited for tasks that involve data processing, signal processing, and real-time systems.
Moore Machines
On the other hand, Moore Machines generate output based only on the current state and do not consider the input symbol during transitions. This means that the output remains constant during the time the FSM is in a particular state and only changes when the machine transitions to a different state.
Moore Machines are commonly used in applications where the output depends solely on the current internal state of the system. They are well-suited for tasks where the output is driven by the state’s characteristics and does not require immediate responsiveness to changes in input symbols.
How do Finite-State Machines work?
Finite-State Machines (FSMs) work on a simple and elegant principle, which involves transitioning between different states based on the input symbols they receive.
Let’s break down the process step by step.
States and transitions
At the heart of a Finite-State Machine are the states. A state represents a specific condition or situation that the machine can be in at any given moment. For example, imagine a traffic light with three states: “Red,” “Yellow,” and “Green.” Each of these states represents a different condition of the traffic light.
The FSM also has transitions, which define how it moves from one state to another based on the input it receives. Transitions are typically triggered by input symbols. These symbols can be anything from letters, numbers, or any other symbols relevant to the application of the FSM.
Initial state
When a Finite-State Machine starts its operation, it begins in an initial state. The initial state is the starting point of the machine’s computation. It serves as the entry point for the FSM to begin processing the input.
Reading input symbols
Once the Finite-State Machine is in the initial state, it starts reading input symbols one by one. The machine reads an input symbol from the input stream, processes it, and then proceeds to read the next input symbol.
Transition rules
For every state and input symbol combination, there are predefined transition rules that dictate how the FSM should respond. These rules determine the next state the machine should transition to when it encounters a specific input symbol in a given state.
To illustrate this, let’s consider a simple FSM with three states: “A,” “B,” and “C,” and two input symbols: “0” and “1.” The transition rules for this FSM could be:
- If the FSM is in state “A” and receives input symbol “0,” it transitions to state “B”
- If the FSM is in state “A” and receives input symbol “1,” it remains in state “A”
- If the FSM is in state “B” and receives input symbol “0,” it transitions to state “C”
- If the FSM is in state “B” and receives input symbol “1,” it remains in state “B”
- If the FSM is in state “C” and receives input symbol “0,” it transitions back to state “A”
- If the FSM is in state “C” and receives input symbol “1,” it transitions to state “B”
Transitioning between states
As the FSM reads each input symbol, it applies the transition rules to determine the next state. It follows the defined transitions until it reaches a final state or halts.
Final states and halting
A Finite-State Machine can have one or more final states. When the FSM reaches a final state after processing the input symbols, it signifies that it has completed its task or reached a specific goal. The machine may then produce an output or trigger some action associated with that final state.
Alternatively, the FSM may halt without reaching a final state if it encounters an input symbol for which no valid transition rule is defined. In this case, the FSM may stop its operation without completing the task it was designed for.
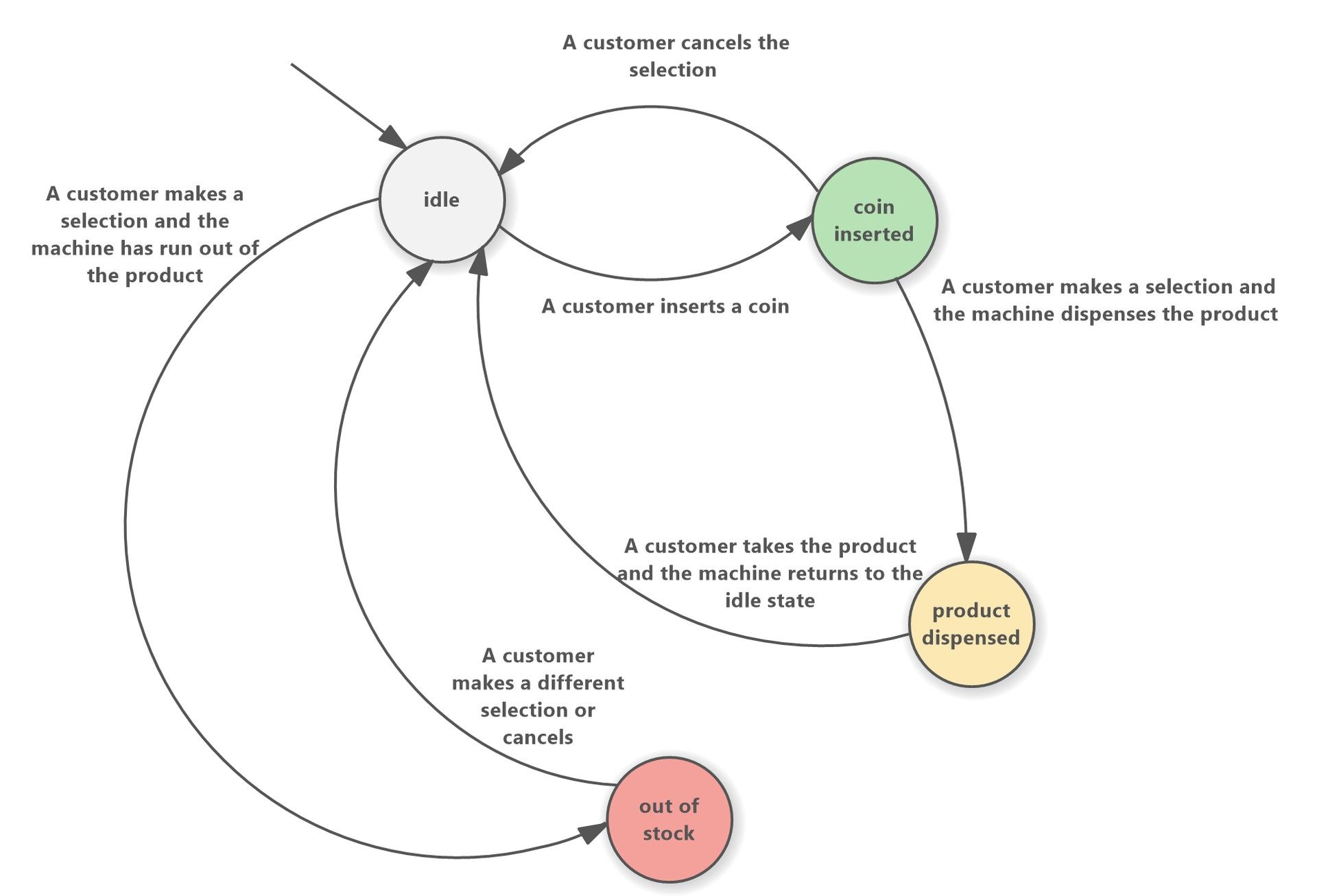
Finite State Machines are much more than simple vending machines
Finite-State Machines (FSMs) have proven to be versatile tools with applications across various fields. Their simplicity, efficiency, and ability to model sequential behaviors make them valuable in diverse domains.
Control of machines and devices
Finite-State Machines play a vital role in controlling various machines and devices by specifying their behavior based on inputs. In this context, FSMs act as decision-making units that govern the actions of machines. For instance, in industrial automation, FSMs can be used to control complex processes in manufacturing plants.
The FSM defines the different states that the machinery can be in, such as “Idle,” “Processing,” and “Shutdown.” Based on sensor inputs and other external factors, the FSM transitions between these states, controlling the machine’s operations and ensuring efficient functioning.
Computer programming
In software development, FSMs are widely employed for various tasks. One common application is lexical analysis, where Finite-State Machines help tokenize source code into meaningful components such as keywords, identifiers, and operators.
The FSM processes the input stream character by character, transitioning between states to identify and extract the appropriate tokens. Additionally, FSMs are used for parsing, where they analyze the syntax of a program based on a grammar, and for regular expression matching, where they match patterns in strings efficiently.
Automated systems
FSMs are an integral part of automation systems, enabling efficient and reliable control over processes. In manufacturing, FSMs are used to manage assembly lines, monitor product quality, and optimize production workflows.
Automation processes rely on FSMs to make decisions, trigger actions, and ensure that tasks are carried out systematically and without errors.

Communication protocols
Communication protocols often utilize FSMs to handle data transmission and error handling. For instance, in networking protocols like TCP/IP, FSMs manage the establishment and termination of connections between devices.
FSMs ensure that data packets are transmitted correctly, and if errors occur during transmission, the FSM handles the retransmission of lost data to maintain data integrity and reliability in the communication process.
Robotics
FSMs are essential in defining the behavior and decision-making processes of robots in various scenarios. Robots operate in dynamic and unpredictable environments, and Finite-State Machines provide a structured approach to model their responses to sensory inputs and external stimuli.
For example, in a mobile robot navigating through a maze, an FSM can guide its movements based on sensor inputs, enabling it to make decisions about its path, avoid obstacles, and reach its destination efficiently.
Artificial intelligence
Finite-State Machines serve as the predecessors to more complex AI technologies, laying the foundation for sequential decision-making in AI systems. While Finite-State Machines themselves have limitations in handling highly complex and dynamic tasks, they have influenced the development of more advanced AI models and algorithms.
Sequential decision-making, a key aspect of AI systems, draws inspiration from the principles of FSMs, where a series of decisions lead to a specific outcome based on input signals.
Development of games
Finite-State Machines are used to control characters’ behavior, handle game states, and manage game logic. Games often involve characters with specific behaviors and interactions. FSMs provide a structured way to define these behaviors and enable characters to respond to player inputs and game events appropriately.
FSMs can represent the different states of a character, such as “Idle,” “Running,” “Jumping,” and “Attacking,” and transition between these states based on player actions and game events, creating engaging and dynamic gameplay experiences.
One can’t help but wonder if Edward Forrest Moore ever imagined that this simple but inspiring algorithm he created would gift humanity with this technology in 2023.
While we wait with curiosity to see what more AI and robotics can achieve, we pay our respects to him.
Featured image credit: Photo by Chris Briggs on Unsplash.