Today we are delving into what is linear regression in machine learning. Linear regression is both a statistical and a machine learning algorithm. Linear regression analysis estimates the value of one variable relative to the value of another. Linear regression is frequently used in statistical data analysis.
Most machine learning algorithms are borrowed from various fields, primarily statistics. Anything that can help models predict better will eventually become part of machine learning. So, we can say that linear regression is a statistical and machine learning algorithm.
Linear regression is a popular and uncomplicated algorithm in data science and machine learning. In addition to being a supervised machine learning algorithm, it is the simplest regression form used to examine the statistical relationship between variables.
What is linear regression in machine learning?

Linear regression is a statistical method that tries to show the relationship between variables. This method looks at different data points and draws a trendline—for example, the increasing repair cost of a piece of machinery over time.
This form of analysis estimates the coefficients of the linear equation using one or more independent variables that best predict the value of the dependent variable. Linear regression sits on a straight line or surface that minimizes mismatches between predicted and actual output values.
Again, linear regression is used to determine the character and strength of the relationship between the dependent variable and several other independent variables. It can also help build models to predict stock prices.
Before attempting to fit a linear model to the observed dataset, it should be evaluated whether there is a relationship between the variables. Of course, this does not mean that one variable causes the other. However, there must be a visible correlation between them. For example, it is not true that someone with higher college grades will receive a higher salary. However, there may still be a relationship between the two variables.
Correlation coefficients are used to calculate how strong the relationship between two variables is. It is usually denoted by “r” and has a value between -1 and 1. A positive correlation coefficient value indicates a positive relationship between variables. Similarly, a negative value indicates a negative relationship between the variables.

Linear regression types
There are two types of linear regression: simple linear regression and multiple linear regression.
Simple linear regression
Simple linear regression finds the relationship between a single independent variable and a corresponding dependent variable. The independent variable is the input, and the corresponding dependent variable is the output.
Multiple linear regression
Multiple linear regression finds the relationship between two or more independent variables and their corresponding dependent variable. There is also a special method of multiple linear regression called polynomial regression.
A simple linear regression model may have only one independent variable, while a multiple regression model may have two or more independent variables. And yes, other nonlinear regression methods are used for highly complex data analysis.
Additionally, you can run the linear regression technique in various programs and environments, including R linear regression, MATLAB linear regression, Sklearn linear regression, Python linear regression, and Excel linear regression.
What does linear regression do?
Linear regression models are relatively simple and provide an easy-to-interpret mathematical formula that can produce predictions. Linear regression can be applied to various fields in business and academic studies.
You can see linear regression in everything from the biological, behavioral, environmental, and social sciences to business. Linear regression models, which have become scientifically proven, can reliably predict the future.
Business and organizational leaders can make better decisions using linear regression techniques. Organizations ultimately collect and store large amounts of data. Linear regression, on the other hand, helps them use this data to manage better reality, rather than relying on experience and intuition. They can take large amounts of raw data and turn it into actionable information.

Differences between logistic regression and linear regression
While linear regression estimates the continuous dependent variable for a given set of independent variables, logistic regression estimates the categorical dependent variable.
Both are supervised learning methods. However, linear regression is used to solve regression problems, while logistic regression is used to solve classification problems.
Logistic regression can solve regression problems. But mainly, this is used in classification problems. Its output can only be 0 or 1. It is valuable in situations where you need to determine the probabilities between two classes or, in other words, calculate the probability of an event. For example, logistic regression can predict whether it will rain today.
Linear regression assumptions
When using linear regression to model the relationship between variables, you can make a few assumptions. Assumptions are conditions that must be met before a model is used to make predictions.
There are four general assumptions for linear regression models:
- Linear relationship: A linear relationship exists between the independent variable “x” and the dependent variable “y”.
- Independence: The variables are independent. There is no relationship between consecutive residuals in time series data.
- Homoscedasticity: The variables have equal variants at all levels.
- Normality: The variables are normally distributed.
Advantages and disadvantages of linear regression
Linear regression is one of the simplest algorithms to understand and implement. It’s also a great tool for analyzing relationships between variables.
The advantages of linear regression
It is a go-to algorithm because of its simplicity.
- Although it is susceptible to overfitting, it can be avoided with the help of size reduction techniques.
- Interpretable.
- It is linearly separable and performs well on datasets.
- Space complexity is low. Therefore, it is a high-latency algorithm.
However, linear regression is generally not recommended for most practical applications. This is because it oversimplifies real-world problems by assuming a linear relationship between variables.

The disadvantages of linear regression
- Outliers can have negative effects on the regression.
- It assumes a linear relationship between variables, as there must be a linear relationship between the variables for it to fit a linear model.
- It detects that the data is normally distributed.
- It also looks at the relationship between the mean of the independent and dependent variables.
- Linear regression is not a complete description of the relationships between variables.
- The presence of a high correlation between variables can significantly affect the performance of a linear model.
In linear regression, it is important to evaluate whether the variables have a linear relationship. While some try to guess without looking at the trend, it’s best to ensure a moderately strong correlation between the variables.
As we mentioned, looking at the scatterplot and correlation coefficient are excellent methods. Even if the correlation is high, looking at the scatterplot is a necessary check. If the data is visually linear, linear regression analysis can be performed.
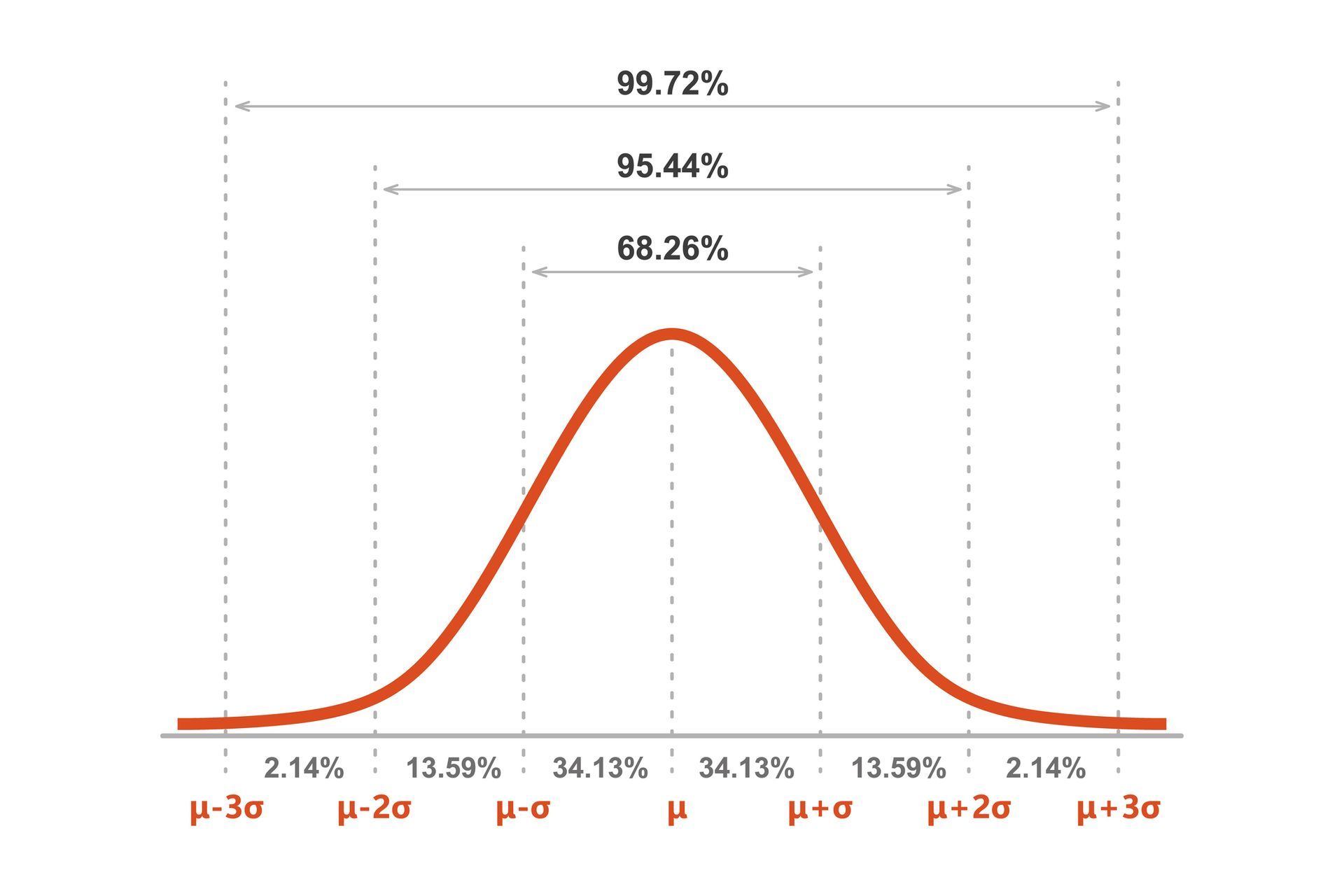
How to make the most of linear regression?
Linear regression requires data preparation and preprocessing as other machine learning models. Missing values, mistakes, outliers, anomalies, and a lack of attribute values will all be present. Here are some ideas for dealing with missing data and creating a more trustworthy prediction model.
The purpose of linear regression is to assess the impact of one or more variables on another. Because the predictor and response variables are thought to be clean, Least Squares Regression sees them as noise-free. Removing noise with several data cleaning techniques is critical in this case. If you can, remove the outliers from the output variable.
Also, linear regression will perform better if the input and output variables have a Gaussian distribution and normalized or standardized input variables. If the data has many features, you’ll need to transform it so that it has a linear relationship. Linear regression will overfit the data if the input variables are highly correlated. Collinearity must be eliminated.





