Quantum Machine Learning (QML) is a young theoretical research discipline exploring the interplay of quantum computing and machine learning approaches. In the last couple of years, several experiments demonstrated the potential advantages of quantum computing for machine learning.
The overall goal of Quantum Machine Learning is to make things move more quickly by combining what we know about quantum computing with traditional machine learning. The concept of Quantum Machine Learning arises from classical Machine Learning theory and is interpreted from that perspective.
Search for an impact
In recent years, quantum computing’s development in theory and practice has advanced quickly, with the potential benefit in real applications becoming more apparent. One key area of study is how quantum computers might impact machine learning. It is recently proven experimentally that quantum computers can naturally solve specific problems with complex correlations between inputs that are extraordinarily difficult for conventional systems.
Quantum computers may be more useful in specific fields, according to Google’s research. Quantum models created on quantum computers may be far more potent for select applications, potentially offering faster processing and generalization on less data. As a result, it is critical to determine when such a quantum advantage can be obtained.
The notion of quantum advantage is often expressed in terms of computational benefits. Can a quantum computer create a more accurate result in the same amount of time as a traditional machine with some well-defined input and output problems?
Quantum computers have impressive advantages for several algorithms, such as Shor’s factoring algorithm for factorizing large primes or the quantum simulation of systems. However, data availability might dramatically impact how difficult the problem is to solve and how beneficial a quantum computer may be. Understanding when a quantum computer can help in machine learning depends on the task and the available data.
Let me refresh your basic ideas before we take on an adventure through labs and theoretical ideas to explore how quantum computing will change the future of machine learning.
What is quantum computing?
Quantum computing is a method for performing calculations that would otherwise be impossible with conventional computers. A quantum computer works by utilizing qubits. Qubits are similar to your regular bits found in a PC, but they can be put into a superposition and share entanglement.
Classical computers can execute deterministic classical operations or generate probabilistic processes using sampling techniques. Quantum computers, on the other hand, can utilize superposition and entanglement to perform quantum computations that are almost impossible to replicate at scale with conventional computers.
What is machine learning?
Machine learning is a form of artificial intelligence that focuses on applying data and algorithms to mimic human learning for machines to improve their accuracy in predicting outcomes. Historical data is fed into machine learning algorithms to generate new output values.
Organizations use machine learning to gain insight into consumer trends and operational patterns, as well as the creation of new products. Many of today’s top businesses incorporate machine learning into their daily operations. For many businesses, machine learning has become a significant competitive differentiator. In fact, machine learning engineering is a rising area.
Google’s quantum beyond-classical experiment proved that it is possible to complete a calculation in 200 seconds on a 53 noisy qubits quantum computer, which would take 10,000 years using current algorithms on the world’s most powerful classical computer. This is the beginning of a new era in computing, known as the Noisy Intermediate-Scale Quantum (NISQ) era. Quantum computers with hundreds of noisy qubits are anticipated to be developed in the near future.

Building blocks of Quantum Machine Learning
Quantum Machine Learning (QML) is based on two foundations: quantum data and hybrid quantum-classical models:
Quantum data
Any data source in a natural or artificial quantum system is regarded as quantum data. Quantum data exhibits superposition and entanglement, which lead to joint probability distributions that would require an exponential number of conventional computational resources to represent or maintain. The data generated by NISQ processors are noisy and usually entangled just before the measurement. Heuristic machine learning extracts useful classical information from noisy entangled data.
Superposition States
Remember how we talked about quantum computing using “qubits” instead of “bits”? A bit is a binary digit, and it serves as the basis of conventional computing. The term “qubit” refers to a Quantum Binary Digit. Qubits can be in multiple states simultaneously, unlike bits, which can only have two states: 0 and 1.
Imagine you tossed a coin. A coin has two sides: Heads (1) or Tails (0). We do not know which side the coin is on until we stop it or hit the ground after it’s in mid-air. However, if you look closer, you will notice which side it is on for that time. Depending on your viewpoint, the coin indicates both 0 and 1; it displays just one side only if you stop it to examine.
The same idea applies to qubits and is called the superposition of two states. The superposition implies that there is a chance the qubit is in several states at once. When we get our result after a coin toss, the superposition dissipates.
Entanglement
The concept of quantum entanglement states that if we take two qubits, they will always be in a superposition of two states. When one is in a spin-up state, the other is immediately in a spin-down state. There is no scenario under which both qubits are in the same state. In other words, they are always entangled. This phenomenon is known as quantum entanglement.
A quantum neural network (QNN) is a parameterized quantum computational model
ideally carried out on a quantum computer
Hybrid models
A quantum model may represent and generalize data with a quantum mechanical origin. But quantum models cannot generalize quantum data using conventional computers alone because near-term quantum processors are still tiny and noisy. Combining NISQ processors with conventional co-processors to create powerful machines has been around for a long time. To be effective, NISQ processors must work in tandem with classical co-processors.
What did Google prove exactly?
In the “Power of Data in Quantum Machine Learning” paper published in Nature Communications, Google examined the issue of quantum advantage in machine learning to determine when it will be relevant. Google researchers explored how the complexity of a problem varies with the amount of data available and how this can sometimes allow classical learning models to compete against quantum algorithms. They then constructed a working screening strategy when one of the data embedding parameters has a qubit advantage in the kernel context.
Researchers utilized the findings from the testing procedure and learning bounds to produce an innovative approach that transmits selected aspects of feature maps from a quantum computer into classical space via projection. As a result, they have developed an approach to applying machine learning to the quantum experience that incorporates insights from classical machine learning and shows how the best empirical separation in quantum learning benefits.
We have mentioned how the idea of quantum advantage over a classical computer is often framed in terms of computational complexity classes. Bounded quantum polynomial time (BQP) problems are believed to be easier to solve by quantum computers than by classical ones, such as factoring large numbers and simulating quantum systems. On the other hand, problems easily solved on classical computers are called probabilistic polynomial (BPP) problems.
Data changes everything
Google’s research showed that learning algorithms equipped with data from a quantum process, such as a natural process like fusion or chemical reactions, form a new class of problems (called BPP/Samp) that can efficiently perform some tasks that traditional algorithms without data cannot, and is a subclass of the problems efficiently solvable with polynomial sized advice (P/poly). This demonstrates that understanding the quantum advantage for some machine learning tasks requires looking at existing data in some cases.
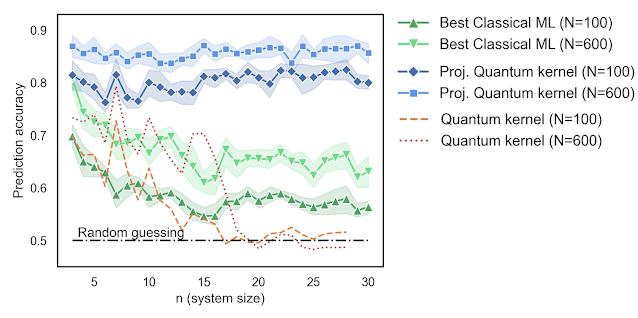
Google has demonstrated that the availability of data has a significant impact on the question of whether quantum computers can aid in machine learning. They developed a practical set of tools for examining these questions and used them to develop a new projected quantum kernel method with many advantages over existing approaches.
Researchers establish towards the greatest numerical demonstration yet, 30 qubits of quantum embeddings’ learning benefits. While a full computational benefit on a real-world application has yet to be seen, this research lays the groundwork for future progress.

Quantum kernels handle “unsolvable” ML problems
Several quantum machine learning algorithms have postulated exponential speedups over traditional machine learning techniques by assuming that one can offer conventional data to the algorithm in quantum states.
There have been many attempts at quantum machine learning algorithms that can be referred to as “heuristics,” implying that their efficacy has no formal proof. Researchers seek ways to tackle this problem by exploring approaches that align with the actual-world needs of data access, storage, and processing. Havlíček et al.’s proposal for quantum-enhanced feature spaces, also known as quantum kernel algorithms, shows promise.
Despite the popularity of these quantum kernel approaches, the most crucial question is remains the same:
Are quantum machine learning algorithms using kernel methods capable of delivering a provable advantage over classical algorithms?
Last year, IBM released a quantum kernel algorithm that, given only classical access to data, gives a provable exponential speedup over classical machine learning techniques for a specific category of classification problems. The most fundamental issues in machine learning are classification errors. They start with training an algorithm on a set of data, known as a training set, where data points have one of two labels. After the training phase, there is a testing phase in which the algorithm must identify a new data point that has never been encountered before.
A simple example is when we provide a computer with photographs of dogs and cats, and it determines whether future photos are of dogs or cats based on this data. The goal of a practical quantum machine learning algorithm for classification should be to provide a correct label in a time that scales polynomially with the size of the data.
IBM proved that quantum kernel methods are superior to classical ones for a particular classification task. The algorithm is based on a quantum kernel approach. It uses a time-tested traditional machine learning technique to learn the kernel function, which locates the important features in the data for classification. The key to its quantum advantage is that we can build a family of data for which only quantum computers can recognize the inherent labeling patterns. Still, for conventional computers, the data appears like random noise.
IBM proved the advantage by tackling a well-known issue that divides conventional and quantum computation: computing logarithms in a cyclic group, where you can generate all group members with a single mathematical operation. The discrete log problem—is a difficulty that arises in cryptography and can be solved on a quantum computer by utilizing Shor’s well-known method, which is thought to require superpolynomial time on a normal computer.
Quantum neural networks: A myth or a reality?
Artificial neural networks (ANN) are a type of neural network model that has been extensively used in classification, regression, compression, generative modeling, and statistical inference. You can also read about the history of neural networks here. Their common feature is linear operations alternating with nonlinear transformations (such as sigmoid functions), which may be pre-determined or learned during training.
Fundamental concerns about the efficacy of neural networks have persisted, despite their success in many areas over the last decade. Are there any strict guarantees for their optimization and the predictions they give? Although they may overfit training data effectively, how do they achieve good cross-generalization performance?
In the QML literature, ANNs have received significant attention. The primary research directions have been to speed up the training of traditional models and to construct networks in which all the parts, from single neurons to learning algorithms, are run on a quantum computer (a so-called “quantum neural network”).
The first research on quantum neural networks was published in the 1990s, and there have been several papers about it. The limitations encountered when attempting to succeed in this area may be attributed to the fundamental distinctions between quantum mechanics’ linearity and the essential function of nonlinear components in ANNs or the fast developments occurring within classical ANNs.
The first research on quantum neural networks
was published in the 1990s
The study of accelerated training of neural networks using quantum resources has focused primarily on restricted Boltzmann machines (RBMs). BMRs are generative models (i.e., models that allow new observational data to be generated based on prior knowledge) suited to be studied from a quantum perspective owing to their strong connections with the Ising model.
It has been shown that computing the log-likelihood and sampling from an RBM is computationally hard. Unfortunately, many MCMC methods have drawbacks that make them unsuitable for this purpose. However, even with MCMC, sample drawing might be costly for models with numerous neurons. Quantum resources may help to reduce the cost of training.
There are two primary categories of quantum algorithms to teach RBMs. The first is based on approaches from quantum linear algebra and quantum sampling. Three algorithms were developed by Wiebe to effectively train an RBM using amplitude amplification and quantum Gibbs sampling. The second variant is more adaptive to change because it requires a quadratic lesser number of examples to train the RBM, but its scaling in terms of edges is far worse than contrastive divergence.
This method’s other advantage is that it may be used to train full Boltzmann machines (an earlier version of this algorithm was developed). A complete Boltzmann machine is a type of Boltzmann machine where the neurons correspond to the nodes of a complete graph (i.e., they are fully connected). Although full Boltzmann machines have more parameters than RBMs, they are not used in practice due to the high training cost, and, to date, the true potential of large-scale, full Boltzmann machines is unknown.
The second approach for teaching RBMs is based on QA, a quantum computation model encodes issues in an Ising model’s energy function. Use a quantum annealer to generate spin configurations, then train an RBM with those. These are physical implementations of RBMs, which come with their problems. The effective thermodynamic temperature of the physical machine is a problem.
To overcome this problem, they introduced an algorithm to estimate the effective temperature and benchmarked the performance of a physical device on some simple problems. A second critical analysis of RBMs’ quantum training showed with numerical models how the limitations that the first-generation quantum machines are likely to have, in terms of noise, connectivity, and parameter tuning, severely limit the applicability of quantum methods.
Quantum computers can be used and trained like neural networks, so we can achieve Quantum Machine Learning
A hybrid approach between training ANNs and a fully quantum neural network is the quantum Boltzmann machine proposed. In this model, the standard RBM energy function gains a purely quantum term (i.e., off-diagonal) that, according to the authors, allows a more affluent class of problems to be modeled (i.e., problems that would otherwise be hard to model classically, such as quantum states).
Whether these models can provide any advantage for classical tasks is unknown. Researchers believe that quantum Boltzmann machines might help reconstruct a quantum state’s density matrix from measurements (this operation is known in the quantum information literature as “quantum state tomography”).
Conclusion: We are close to Quantum Machine Learning
Although there is no agreement on the characteristics of a quantum ANN, research in the last two decades has aimed to create networks composed only of quantum-mechanical laws and features. In particular, most of the papers failed to reproduce basic features of ANNs (for example, the attractor dynamics in Hopfield networks). On the other hand, it can be argued that the single greatest challenge to a quantum ANN is that the quantum mechanics is linear, but ANNs require nonlinearities.
The two proposals recently solved the problem of modeling nonlinearities by employing measurements and including multiple overhead qubits in each node’s input and output. However, these models still lack some important features of a fully quantum ANN. For example, the model parameters remain classical, and it is impossible to prove that the models can converge with a polynomial number of iterations. The papers’ authors acknowledge that, in their current forms, the most-likely applications of these theories appear to be the learning of quantum objects rather than the improvement of classical data. Finally, we observe no attempts to model nonlinearities directly on amplitudes thus far.





